VISUAL INFORMATION OF THE MODE FORMATION IN ACCELERATING TAYLOR VORTEX FLOW WITH FINITE LENGTH

H. FURUKAWA1, T. WATANABE2 and I. NAKAMURA3

Keywords : Formation process, Taylor vortex flow, Non-uniqueness, Non-linear phenomena

Abstract

As a paradigm of non-linear systems, we numerically study and visualize Taylor vortex flow between two concentric rotating cylinders with finite length. The governing equations are the unsteady Navier-Stokes equations. The outer cylinder wall and the upper and lower end walls of the gap are stationary, and the inner cylinder begins to rotate with constant accelerations. The main parameters which determine the modes of the Taylor vortex flow are the aspect ratio and the Reynolds number. The former is defined by the ratio of the cylinder length to the gap between cylinders, and the latter is determined by the inner cylinder speed as the representative velocity. We have found that, when the aspect ratio and the Reynolds number are fixed, the final modes of flows depend on the acceleration rate of the inner cylinder. Even though the same modes appear under the fixed aspect ratio and the Reynolds number, the developing processes may be different. This indicates that the acceleration rate of the inner cylinder significantly influences the final mode of flows between cylinders with finite length.

1 Introduction

After Benjaminfs [1] study, the Taylor vortex flow between two concentric rotating cylinders with finite length has been investigated from various viewpoints. The aspect ratio ? and the Reynolds number Re are considered as the main parameters which determine the modes of the Taylor vortex flow [2][3][4]. The aspect ratio ? is defined as the ratio of the cylinder length to the gap between cylinders, and the Reynolds number Re is based on the rotation speed of the inner cylinder. One major character in the Taylor vortex flow is its non-uniqueness. The difference of the inner cylinder acceleration rate causes the various modes, even though the aspect ratio and the Reynolds number are fixed. Alziary de Roquefort and Grillaud [5] analyzed numerically the non-uniqueness by using steady axisymmetric Navier Stokes equations formulated by the finite difference method. Lücke et. al. [6][7] used the unsteady equations, and they reported that Ekman-vortices which develop on the stationary end walls cause the bulk Taylor vortex flow. Kuo and Ball [8] conducted their three dimensional numerical simulation, and they found the steady modes when the rotational speed of the inner cylinder was gradually increased from zero. Bielek et. al. [9] observed experimentally the formation of Taylor vortices after sudden starts of the inner cylinder. They did not state the mode formation processes and the effect of the acceleration rate of the inner cylinder. In this study, the flow visualization numerically demonstrates the mode formation process of the Taylor vortex flow between two concentric cylinders. Under the condition that the aspect ratio and the Reynolds number are fixed, the speed of the inner cylinder is increased from zero at various acceleration rate. We also have investigated the mode formation process from the sudden-start of the inner cylinder in the case that ? and Re are varied [10].

2 Numerical method

The governing equations are the unsteady axisymmetric Navier-Stokes equations and the equation of continuity, which are expressed in the cylindrical coordinates (r, ?, z) and velocity components (u, v, w) respective directions.

(1)

Staggered grid is used in this calculation. The number of grid points in the radial direction is 41, and the number of grid points in the axial direction is determined by the proportionality to the cylinder length with 42 points for an aspect ratio of unity. The number of grid points used in the present calculation is estimated thick enough not to influence the results, and the time interval fills the CFL conditions. The basic solution procedure is the MAC method, and the time integration is the Euler explicit method. The spatial differentiation is the QUICK method for convection terms and the second-order central difference method for other terms. All physical parameters are made dimensionless by using the characteristic length which is the gap between cylinders, the characteristic velocity which is the maximum circumferential rotation speed attained during each calculation, and the characteristic time defined as the ratio of the characteristic length to the characteristic velocity. The inner cylinder speed is accelerated from zero at various rate. The initial conditions are that all velocity components are zero in the entire domain. The outer cylinder side, the upper edge and lower cylinder edge are stationary. The boundary conditions at the cylinder walls and both end walls are no-slip conditions for velocity components and Neumann conditions for pressure which are obtained from momentum equations. The Stokes stream function ? is used for visualizing the calculated results.

3 Results

Table 1 shows the modes of the Taylor vortex flow in the case that the inner cylinder is accelerated at various rate at ? = 4.0 and Re = 1000. Each column of the table indicates the non-dimensional acceleration time T, flow mode and the mean kinetic energy E in (r, z) plane, which is defined by

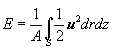(2)

where S is an integral domain and A is the area of a meridional section.

At ? = 4.0 and Re = 1000, three different modes appear, which depend on the acceleration time of the inner cylinder: the anomalous four-cell mode (A4), the normal four-cell mode (N4) and the normal two-cell mode (N2). The mean kinetic energy E is same if the final mode is same. As an example of mode formation processes, Fig. 1 shows the mode formation processes to the normal two-cell mode at T = 120. In the figure, the rotating inner cylinder is on the left and the stationary outer cylinder is on the right. Figure 1 illustrates the time variations of ? counters in the (r, z) plane. The warm color area shows a vortex rotating in a clockwise direction and a vortex rotating in a counter-clockwise direction is shown cold color area. First, the vortices develop from the inner upper and the inner lower corners of the cylinders. Then the vortices grow in the axial direction, and the flow field has ten vortices. Finally, the top and bottom vortices enlarge, and flow field becomes the normal two-cell mode.

To determine the number of vortices quantitatively, Fig. 2 shows the power spectrum of the integrated ? in the radial direction, which is determined by.

(3)

where D is the gap length between cylinders and P is the finite domain in the axial direction. The dominant frequency shifts from 2 to 4, 5 and 1. The flow mode is established about t = 40. From this, we can say quantitatively that the flow field has two vortices.

Figure 3 indicates the mode formation processes of the normal two-cell mode at ? = 4.0, Re = 1000 and T = 240, which are the same conditions as the ones in the Fig. 1 except that T is doubled. The final mode is the normal two-cell mode, which is same as Fig. 1, but the formation process is different. In Fig. 3, the flow field has the normal six-cell mode, and begin to oscillate. Then the second vortex from the top and the second vortex from the bottom weaken, and they finally disappear. The cells adjacent to the disappearing cells rotate in the same direction. So, they can not be stable when their boundaries are attached. Therefore, the cells adjacent to the disappearing cells finally disappear. Finally, the flow field becomes the normal two-cell mode. Because the flow field has same mode as the one in Fig. 1 and 3, the mean kinetic energy E is the same in these cases. Non-uniqueness means that the flow field has different modes at same ? and Re. Now we find new non-uniqueness of the Taylor vortex flow that the mode formation processes are different, even though the flow field has the same final mode. We also confirm non-uniqueness in the mode formation processes of the normal four-cell mode ( T = 6 and 300 ) and the anomalous four-cell mode ( T = 3 and 60 ).

In the mode formation processes of the normal two-cell mode shown in Fig. 1 and 3, the vortices develop from the inner upper and the inner lower corners of the cylinders. We also observed that the vortices developing from the mid-plane in the axial direction grow earlier than the vortices from the inner upper and the inner lower corners. In Table 1, the figures between parentheses in the middle column show the mode formation process types. The same figure shows that the flow field grows in the same formation processes.

4 Conclusions

The Taylor vortex flow between two concentric rotating cylinders with finite length has been investigated using the numerical flow visualization, and following results are obtained.

1. The non-uniqueness of the Taylor vortex flow is found numerically in the case that the acceleration rate of the inner cylinder speed is varied.

2. The mode formation processes may be different even though the flow fields have the constant mode at constant ? and Re.

3. Besides the vortices developing from the inner upper and the inner lower corners, the vortices developing around the mid-plane in the axial direction are observed.

5 REFERENCES

  1. Benjamin, T. B.: Bifurcation phenomena in steady flows in a viscous flow - II. Experiment-, Proceedings of the Royal Society of London, Series A, Vol. 359, pp. 27-43, 1979.
  2. Cliffe, K.A.: Numerical calculation of two-cell and single cell Taylor flow, Journal of Fluid Mechanics, Vol. 135, pp. 219-233, 1983.
  3. Cliffe, K. A.: Numerical calculation of the primary flow exchange process in the Taylor problem, Journal of Fluid Mechanics, Vol. 197, pp. 57-79, 1988.
  4. Bolstad, J. H., and Keller, H. B.: Computation of anomalous modes in the Taylor experiment, Journal of omputational Physics, Vol. 69, pp. 230-251, 1987.
  5. Alziary de Roquefort, T. and Grillaud, G.: Computation of Taylor vortex flow by a transient implicit method, Computers and Fluids, Vol. 6, pp. 259-269, 1978.
  6. Lücke, M., Mihelicic, M. and Wingerath, K.: Flow in a small annulus between concentric cylinders, Journal of Fluid Mechanics. 140, pp. 343-353, 1984.
  7. Lucke, M., Mihelcic, M. and Wingerath, K.: Front propagation and pattern formation of Taylor vortices growing into unstable circular couette flow, Physical Review, A, Vol. 31, No. 1, pp. 396-409, 1985.
  8. Kuo, D.C. and Ball, K.S.: Taylor-Couette flow with buoyancy: onset of spiral flow, Physics of Fluids, Vol. 9, No. 10, pp. 2872-2884, 1997.
  9. Bielek, C.A. and Koschmieder, E.L.: Taylor vortices in short fluid columns with large radius ratio, Physics of Fluids, A 2-9, pp. 1557-1563, 1990.
  10. Watanabe, T., Furukawa, H., Aoki, M. and Nakamura, I.: Visualization of sudden-start flow between two concentric rotating cylinders, Proc. 9th Int. Symp. Flow Visualization (this volume).