(1)
VISUAL INFORMATION OF THE MODE FORMATION IN ACCELERATING TAYLOR VORTEX FLOW WITH FINITE LENGTH
H. FURUKAWA1, T. WATANABE2 and I. NAKAMURA3
Keywords : Formation process, Taylor vortex flow, Non-uniqueness,
Non-linear phenomenonAbstract
As a paradigm of non-linear systems, we numerically study and visualize the Taylor vortex flow between two concentric rotating cylinders with finite length. The governing equations are the unsteady Navier-Stokes equations. The outer cylinder wall and the upper and lower end walls of the cylinders are stationary, and the inner cylinder begins to rotate with a constant accelerations. The main parameters that determine the modes of the Taylor vortex flow are the aspect ratio and the Reynolds number. The former is defined by the ratio of the cylinder length to the gap between cylinders, and the rotation velocity of the representative velocity that is the inner cylinder determines the latter. We have found that, even when the aspect ratio and the Reynolds number are fixed, the final modes of flows depend on the acceleration rate of the inner cylinder. Though the same mode appears under the fixed aspect ratio and the Reynolds number, the developing processes may be different. This indicates that the acceleration rate of the inner cylinder significantly influences the final mode of flows between cylinders.
1 Introduction
After Benjaminfs [1] study, the Taylor vortex flow between two concentric rotating cylinders with finite length has been investigated from various viewpoints.@stigated from various viewpoints.@ The aspect rati? and the Reynolds number Re are considered as the main parameters that determine the modes of the Taylor vortex flow [2][3][4].@ are considered as the main parameters that determine the modes of the Taylor vortex flow [2][3][4].@ The aspect rati? is defined as the ratio of the cylinder length to the gap between cylinders, and the Reynolds number Re is based on the rotation speed of the inner cylinder.@ is based on the rotation speed of the inner cylinder.@ Alziary de Roquefort and Grillaud [5] analyzed numericallthe Taylor vortex flow by using steady axisymmetric Navier-Stokes equations formulated by the finite difference method.@ Lucke et al. [6][7] used the unsteady equations, and they reported that Ekman vortices that develop on the@cke et al. [6][7] used the unsteady equations, and they reported that Ekman vortices that develop on the@stationarend walls cause the bulk Taylor vortex flow when the inner cylinder started to rotate suddenly from rest.@rotate suddenly from rest.@ K and Ball [8] took the effect of the buoyancy into account and conducted the three dimensional numerical simulation.@buoyancy into account and conducted the three dimensional numerical simulation.@ They found the steady modein the case that the rotational speed of the inner cylinder was gradually increased from zero. The Taylor vortex flow has a normal mode and an anomalous mode.@tex flow has a normal mode and an anomalous mode.@ When thend walls of the cylinders are fixed, the normal mode has a normal cell that gives an inward flow in the region adjacent to the end wall.@.@ The anomalous mode has anomalous cell(s) on either or bh end walls.@s.@ The anomalous cell gives an outward flow near the end wall, which is opposite to the flow directiofound in the normal mode.@in the normal mode.@ Bielek et al. [9] observed experimentally thmode formation processes of the Taylor vortices, and@Taylor vortices, and@they have concded that the anomalous three-cell mode never formed directly after sudden start of the inner cylinder but originated from the decay of the anomalous four-cell mode or the six-cell mode.One major character of the Taylor vortex flow is its non-uniqueness.@One major character of the Taylor vortex flow is its non-uniqueness.The difference of the inner cylinder acceleration rate causes various modes, though the aspect ratio and the Reynolds number are fixed.@The difference of the inner cylinder acceleration rate causes various modes, though the aspect ratio and the Reynolds number are fixed.As mention above, a large number of researches have been carried out into the Taylor vortex flow, but little is known about the non-uniqueness of the mode formation processes of the Taylor vortex flow. The effect of the acceleration rate of the inner cylinder on the mode formation processes has not been reported in detail.@.@ When the flow pattern changes,@unsteady variatns of property values such as torque and kinetic energy arise. The unsteady variation carries the potential for the unexpected system destruction.
@Therefore, the analysis and prediction of the mode formation processes is important from the engineering viewpoint. In this study, the two-dimensional flow visualization numerically demonstrates the mode formation processes of the Taylor vortex flow between two concentric rotating cylinders.@cylinders.@ Under the condition that the aspect ratio and the Reynolds number e fixed, the rotation velocity of the inner cylinder is increased from zero at various acceleration rates.@of the inner cylinder is increased from zero at various acceleration rates.The non-unique mode formation processes from the sudden-start of the inner cylinder have also been investigated by us [10].2 Numerical method
All physical parameters are made dimensionless by using the characteristic length that is the gap between cylinders, the characteristic velocity that is the maximum circumferential rotation speed attained during each calculation, and the characteristic time defined as the ratio of the characteristic length to the characteristic velocity.@fined as the ratio of the characteristic length to the characteristic velocity.@ The governing equations are the unsteady axisymmetric Navier-Stokes equations and the equation of continuity, which are expressed in the cylindrical coordinatesr,
?, z),|
|
(1) |
where u is velocity vector with components (u, v, w) in each direction, p is pressure and t is time. Staggered grid is used in this calculation.@Staggered grid is used in this calculation.@ The number of grid pots in the radial direction is 41, and the number of grid points in the axial direction is determined by the proportionality to the cylinder length with 42 points for an aspect ratio of unity.@ts in the radial direction is 41, and the number of grid points in the axial direction is determined by the proportionality to the cylinder length with 42 points for an aspect ratio of unity.@ The number of grid points is estimatelarge enough not to influence results, and the time interval fills the CFL condition.@uence results, and the time interval fills the CFL condition.@ The basic solution procedure is the MAC method, and the time integration is the Euler explicit method.@ The spatial differentiation is the QUICK method for convection terms and the second-orr central difference method for other terms.@ central difference method for other terms.@ The inner cylinder is accelerated linearly from zerduring the non-dimensional accelerating time T.@.@ The initial conditions are that all velocity components are zero in the entire domain.@ The outer cylinder de, the upper end wall and lower end wall are stationary.@de, the upper end wall and lower end wall are stationary.@ The boundary conditions at the cylinder walls and both end walls are no-slip conditions for velocity components, and Neumann conditions for pressure that are obtained from momentum equations.@ T Stokes stream function
|
|
(2) |
To analyze the property of the Taylor vortex flow, we adopt the mean kinetic energy E and the mean enstrophy
? which are defined by|
|
(3) |
|
|
(4) |
where S is an integral domain and A is the area of a meridional section.@ is the area of a meridional section.@ We run the calculations 1210 times a
? from 2.6 to 4.6, Re from 100 to 1000 and 10 different Ts.3 Results
3.1 Mode formation process at
? = 4.0 and Re = 700 Table 1 shows the final modes of the Taylor vortex flow at ? = 4.0 and Re = 700 in the case that the inner cylinder is accelerated linearly from zero during T.@.@ Each column of the table indicates the non-dimensional acceleration timT, flow mode, the mean kinetic energy E and the mean enstrophy ?.@.Depending on the acceleration time of the inner cylinder, three different modes appear: the anomalous four-cell mode (A4), the normal two-cell mode (N2) and the normal four-cell mode@ur-cell mode (A4), the normal two-cell mode (N2) and the normal four-cell mode@ (N4).At the same final mode, the energy E and the enstrophy ? are the same.@.@ Table shows that the various modes appear even when ? and Re are fixed. This has been known as the non-uniqueness of the Taylor vortex flow [1].Figure 1 illustrates the time variations of
Figure 1 (b) indicates the mode formation process of the normal two-cell mode.@n process of the normal two-cell mode.@ The vortices are generated around the mid-planeand at the inner-lower and the inner-upper corners. Then, the flow field becomes the normal six-cell mode.@he flow field becomes the normal six-cell mode After a while, the flow field@, the flow field@begins to oscillate and itecomes the stable normal two-cell mode after a breakdown of four vortices around the mid-plane.
Figure 1 (c) shows the mode formation process of the anomalous four-cell@Figure 1 (c) shows the mode formation process of the anomalous four-cell@mode.The vortices are generated around the mid-plane, at the inner-lower and the inner-upper corners, and the transient mode with eight cells is established.@.Finally, the four vortices around the mid-plane disappear and@he four vortices around the mid-plane disappear and@the flow becomes the stable anomalous four-cell mo.
Figure 1 (d) shows the mode formation process of the normal four-cell@ell@mode.@ The vortices are generateat the inner-lower and the inner-upper corners.@.First, the normal ten-cell mode is formed. Then, the second vortices from the end walls weaken and disappear.@weaken and disappear.The vortices adjacent to the disappearing vortices rotate in the same direction, and they merge into one vortex.@merge into one vortex.Next, the flow field becomes the normal six-cell mode, and the second vortex and the third vortex from the lower cylinder end wall weaken and disappear.@he flow field becomes the normal six-cell mode, and the second vortex and the third vortex from the lower cylinder end wall weaken and disappear.The final mode is the normal four-cell mode.
@Figure 1 (e) illustrates the mode formation process of the normal two-cell@Figure 1 (e) illustrates the mode formation process of the normal two-cell@mode.@ The vortices are generated around the mid-pla, and at the inner-lower and the inner-upper corners, and the normal ten-cell mode appears.@.Then, the eight vortices in the interior region disappear, and the flow field becomes the normal two-cell mode.@ disappear, and the flow field becomes the normal two-cell mode.
Figure 1 (f) shows the mode formation process of the normal four-cell@Figure 1 (f) shows the mode formation process of the normal four-cell@mode.@ Thfirst vortices appear at the inner-lower and the inner-upper corners, and the normal six-cell mode is formed.@Then, the flow field begins to oscillate. After a breakdown of the second and third vortices from the lower cylinder end wall, the flow field becomes the stable normal four-cell mode. Table 2 summarizes the mode formation processes shown in Fig. 1.
To determine the number of vortices quantitatively, we use the time variation of the wave number components of the power spectrum of
|
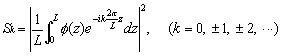 |
(5) |
where D is the gap length between cylinders and L is the cylinder length. When the component at wave number k is dominant, the flow field has 2k vortices. The time variations of Sk are shown in Fig. 2.
Figure 2 (a) indicates the variation in the mode formation process of the anomalous four-cell mode.@ in the mode formation process of the anomalous four-cell mode.@ The dominant wave number shifts from 2 via 3 to 2, anthe flow mode is established about t = 40.@ = 40.@ From this point, we can conclude quantitatively that thfinal flow field has four vortices.@flow field has four vortices.@ The power spectrum helps us to count the number of vortic, and we can investigate the mode formation processes in more detail.@ and we can investigate the mode formation processes in more detail.
Figure 2 (b) shows the time variation of Sk in the mode formation process of the normal two-cell mode.@two-cell mode.The final dominant wave number is one, and the final flow field has two vortices. Figure 2 (c), (d), (e) and (f) show the variation in the formation processes of the anomalous four-cell mode, the normal four-cell mode, the normal two-cell mode and the normal four-cell mode, respectively.@mode and the normal four-cell mode, respectively.The final mode has four, four, two and four vortices, respectively.
3.2 Mode formation process at
? = 4.8 and Re = 1000 Table 3 presents the mode formation processes at ? = 4.8 and Re = 1000.@ = 1000.Depending on the acceleration rate of the@the acceleration rate of the@inner cylind, the flow has five different modes: the anomalous five-cell mode (A5), the anomalous four-cell mode (A4), the anomalous six-cell mode (A6), the normal six-cell mode (N6) and the normal four-cell mode (N4). At ? = 4.8 and Re = 1000, the non-uniqueness of the Taylor vortex flow is found, as is seen at ?@ = 4.0 and Re = 700.@ = 700.@ The normal six-cell mos are not stable, and their kinetic energy and mean enstrophy change with time.@ Figure 3 and 4 show the mode formation processes and the time variation of Sk, respectively.Figure 3 (a) indicates the formation process of the anomalous five-cell mode.@Figure 3 (a) indicates the formation process of the anomalous five-cell mode.@ Firsttwo vortices develop around the mid-plane, and the flow has the normal ten-cell mode.@the mid-plane, and the flow has the normal ten-cell mode.@ext, the vortices attached to the end wall weaken and disappear, and the flow field has the anomalous eight-cell mode.@end wall weaken and disappear, and the flow field has the anomalous eight-cell mode.@ Finally, the anomalous five-cell mo is formed. The time variations of the number of vortices are clearly found in Fig. 4 (a).
The formation processes shown in Fig. 3 are summarized in Table 4. In the formation processes of the anomalous mode, the second vortex divides the normal cell attaching to the cylinder end wall into the inner and the outer regions. The second vortices reach the cylinder end wall, and the flow field becomes the anomalous mode.
3.3 Mode formation process of N6, A3 and A2
Figure 5 and 6 show the flow developments and the time variation of Sk in the formation processes of the normal six-cell mode, the anomalous three-cell mode and the anomalous two-cell mode.@ anomalous two-cell mode.@ Figure 5 (a) indicates the formation process of the normal six-cell mode.@ First, thtwo vortices develop at the inner-lower and the inner-upper corners, and the flow field has six vortices.@, and the flow field has six vortices.@ The six vortices gr gradually, and the developed normal six-cell mode is formed.@.@ Thtime variation of Sk shown in Fig. 6 (a) indicates that the dominant wave number is 3 from the beginning of the mode formation process, and no mode change occurs.@.
Figure 5 (b) shows the formation process of the anomalous three-cell mode.@s of the anomalous three-cell mode.@n the first place, the vortices are generated around the mid-plane, and at the inner-lower and the inner-upper corners, and the flow field becomes the@the inner-lower and the inner-upper corners, and the flow field becomes the@normal six-cell mode.@ Then, the flow field changes from the norm six-cell mode, via the anomalous four-cell mode, to the anomalous three-cell mode.@the anomalous three-cell mode.
Figure 5 (c) presents the formation process of the anomalous two-cell mode.@Figure 5 (c) presents the formation process of the anomalous two-cell mode.The flow field shifts from@he flow field shifts from@the six-cell mo, via the anomalous four-cell mode, to the anomalous two-cell mode.
4 Discussion
At the beginning of the mode formation processes, there are two cases of the development of the vortices.@the development of the vortices.In one case, the vortices develop around the mid-plane.@the mid-plane.In the other case, the vortices develop at the inner-lower and the inner-upper corners.@.In general, the vortices develop around the mid-plane at lower acceleration rate of the inner cylinder, and the vortices develop at the cylinder corners when the acceleration rate is larger.
In the mode formation processes described in Section 3.1, the normal two-cell mode is generated in two ways.@two ways.In one way, the flow field changes from the normal six-cell mode to the normal two-cell mode (Fig. 1 (b)).@.In the other way, the flow field changes from the normal ten-cell mode to the normal two-cell mode (Fig. 1 (e)).@.@ Similarly,@the anomalous four-cell mod(Fig. 1 (a) and (c)) and the normal four-cell mode (Fig. 1 (d) and (f)) have two different mode formation processes, respectively.@.@ Non-uniquenesof the Taylor vortex flow has been used to mean that the flow field has different modes at constant
? and Re.@.@ Now we fina new non-uniqueness of the Taylor vortex flow, which means that the mode formation processes are different even though the flow field has the same final mode.@.We can also find a new non-uniqueness in the formation processes mentioned in Section 3.2 (Fig. 3 (b) and (e).Bielek et al. [9] experimentally concluded that the anomalous three-cell mode never formed directly after sudden start of the inner cylinder, but the mode originated from the decay of the anomalous four-cell mode or from the six-cell mode.@originated from the decay of the anomalous four-cell mode or from the six-cell mode.@ In this study, the anomalous three-cell mode appearat
‘= 2.6, Re= 900 and T= 10.8.@ 10.8.In this case, the flow mode shifts from the normal six-cell mode, to the anomalous four-cell mode, then to the anomalous three-cell mode.@the anomalous three-cell mode.@ The result in this study agrs with Bielek et al.fs experimental observation.@observation.At the fixed
? and Re, the order of the values of the mean enstrophy is listed as A2 < A3, A4 < A6 < N2 < N4 < N6.@A2 < A3, A4 < A6 < N2 < N4 < N6.In general, the mean enstrophy of the normal mode is larger than that of the anomalous mode, and the larger number of vortices the flow field has, the larger the mean enstrophy is.@.@ Howeversome exceptions are found, for example, the enstrophy of the normal two-cell mode (N2) is less than that of the anomalous three-cell mode (A3). Therefore the relation of the mean@ the relation of the mean@enstrophy between mos is not concluded clearly.@clearly.The relation of the mean kinetic energy between modes is not determined, neither.5 Conclusions
The Taylor vortex flow between two concentric rotating cylinders with finite length has been investigated using the numerical flow visualization.@ation.@ The non-uniquenesof the Taylor vortex flow, which has been found in previous studies, is confirmed in the present study. Though the same final mode at constant
? and Re is formed, we found that the mode formation processes may be depend on the acceleration rates of the inner cylinder.@ That is, another modes may be taken during the flow development. At the same final mode, the mean kinetic energy is identical, and so is the mean enstrophy.@the mean enstrophy.@@Thtime variation of the power spectrums of the6 REFERENCES