Comprehensive List of Researchers "Information Knowledge"
Department of Computer Science and Mathematical Informatics
- Name
- YASUMOTO, Masahiro
- Group
- Mathematical Informatics Group
- Title
- Professor
- Degree
- Dr. of Science
- Research Field
- Mathematical logic / Nonstandard arithmetic / Computational complexity

Current Research
Nonstandard Arithmetic and Complexity Classes
OUTLINEWe are promoting research on Mathematical Logic and Theoretical Computer Science. We have been applying the theory of nonstandard models to number theory and the theory of computational complexity.
(1) Nonstandard Arithmetic
The first application of a nonstandard model to mathematics concerned analysis ; nonstandard analysis, initiated by A. Robinson in the 1960s, demonstrated the possibility of using the concept of infinitesimals to serve as a basis for analysis, replacing ε-δ arguments. In the 1970s, A. Robinson and P. Roquette discovered a relationship between the nonstandard models of the rational number field and the structure of function fields embedded in these finite algebraic extensions. The results were used in various number-theoretic studies, including Diophantine equations, a proof of Siegel's theorem on integer points on algebraic curves, and an investigation of Hilbert's irreducibility theorem. Employing further devices, such as iterated nonstandard models, we proved results regarding the range of validity of Hilbert's irreducibility theorem that cannot be obtained by traditional algebraic methods.
(2) Bounded Arithmetic and Computational Complexity
Interest in weak arithmetic has been increasing. In particular, from the mid-1980s, there has been interest in investigating nonstandard models of bounded arithmetic. Bounded arithmetic, introduced by S. Buss, is important as a fundamental mathematical theory for the study of polynomial-time computability classes. Using the nonstandard model of weak arithmetic, it is possible to clearly distinguish between large numbers (numbers represented in binary) and small numbers (numbers used as digit numbers, i.e., the bit length of numbers represented in binary), although in the standard model they are distinguishable as concepts but not as numbers. This method was developed by a forcing method to increase large numbers without increasing small numbers. By extending Boolean algebra to include polynomial-sized Boolean circuits, we study separation problems for the polynomial-time computability class, especially the P=NP problem, considered the most important unsolved problem in the theory of computational complexity. Although developing the oracle part of Boolean-valued extensions has been suggested, no valid theory has yet been established. Problems in the theory of computational complexity can be regarded as problems of the completeness of ideals in the nonstandard model of Boolean algebra. The Boolean-valued extension method can address the P=NP problem from a new perspective. Clearly, the structure of the end extensions of the nonstandard model of weak-bounded arithmetic is closely linked to the separation problem of P and NP or PSPACE. It is Believed that end extensions are longitudinal extensions, while Boolean extensions are lateral extensions. Assuming P=NP or P=PSPACE, we showed that this longitudinal extension has several desirable properties. Meanwhile, using a method similar to a diagonal argument, it has also been demonstrated that certain types of end extensions are impossible. The construction of end extensions is closely related to the definability of bounded oracles of nonstandard models of first-order bounded arithmetic and its consistency with induction. We expect that combining these two methods could prove useful for investigating the separation problems of computational complexity.
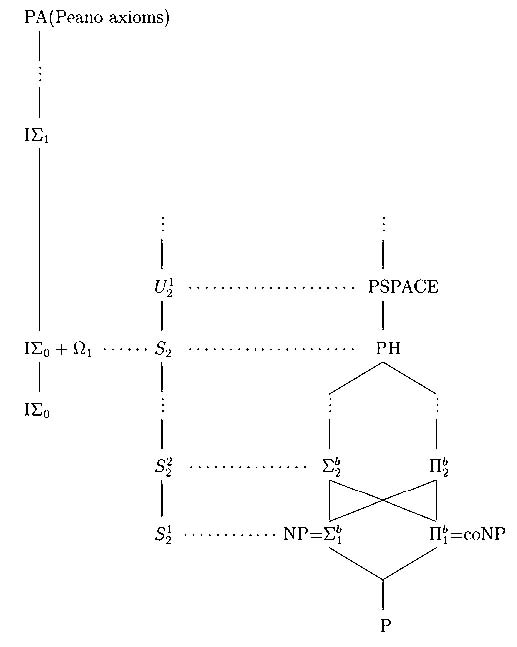
Figure : Bounded arithmetic and complexity classes
Career
- Masahiro Yasumoto received the Dr. of Science Digree in Mathematics from Nagoya University in 1983.
- He was a Research Assoc. at Nagoya University from 1981-1987,
- a lecturer from 1998-1999.
- Since 1999, he has been a Prof. of Human Infomatics and the Informatin Science at Nagoya University.
Academic Societies
- Mathematical Society of Japaan
- Association for Symbolic Logic
Publications
- Separation of first and second order theories i bounded arithmetic, Archive for Mathematical Logic 44 (2005) 685-688.
- Forcing on bounded arithmetic II, Journal of Symbolic Logic 63 (1998) 860-868.
- Nonstandard arithmetic and Hibert subsets, Annals of Pure and Applied Logic 52 (1991) 195-202.








