Comprehensive List of Researchers "Information Knowledge"
Department of Computer Science and Mathematical Informatics
- Name
- KANAMORI, Takafumi
- Group
- Theory of Computation Group
- Title
- Professor
- Degree
- Dr. of Philosophy
- Research Field
- Machine learning / Statistics / Optimization

Current Research
Machine Learning and Statistics
OUTLINEMy research interests cover both statistical inference and computation. In the fields of science, engineering, and social sciences, inferring the model structure behind observed data is crucial. Since data-generating processes are complex and observation is often contaminated by noise, probabilistic models are assumed for data analysis. Many types of statistical techniques have been proposed for data analysis, for example, estimation methods for identifying the probabilistic structure of complex systems, prediction methods for future samples, or testing methods for scientific hypotheses.
In the domain of machine learning, we concentrate on efficient methods of statistical computation for massive data, for example, images, audio data, electroencephalographic data, or text data on the web. These computing techniques are deeply related with other fields in computation sciences such as optimization and algorithms.
TOPICS
(1) Learning Algorithms
In machine learning and statistics, learning algorithms with high prediction accuracy have been developed and studied theoretically. Recently, so-called boosting algorithm, one of ensemble learning algorithms, has received much attention. Boosting is a learning algorithm that combines "weak learner" with low prediction accuracy and constructs learning algorithms with high prediction accuracy. Here, a weak learner denotes learning algorithms with efficient computation instead of low prediction accuracy. From the viewpoint of mathematical statistics, boosting is regarded as a way of inference by weighted least mean square for generalized linear models. On the other hand, boosting algorithms resemble coordinate descent methods in functional spaces. As stated above, boosting algorithms are connected with other research fields. Moreover, some researchers have applied boosting techniques to gene data analysis and successfully identified genes related to diseases.
There are some drawbacks in boosting methods, even if widely applied in data analysis. Especially when huge noises are added in observations, the estimation results are greatly affected by a small amount of outliers. Under these situations, reliable inference is very difficult. We developed robust boosting algorithms that can resist outliers and proved theoretical optimality based on robust statistics.
(2) Information Geometry
In statistical inferences, we commonly assume statistical models for data analysis. The geometrical structure of model is deeply connected with the accuracy of inferences. In information geometry, statistical models are regarded as differentiable manifolds, and the relation between the statistical properties of estimators and the geometrical structures of statistical manifolds is studied. Slightly different from classical Riemannian geometry, the duality of connections derived from the invariance of information has an important role. Such geometrical viewpoints support intuitive understanding of statistical inference and are greatly useful for developing estimation methods in practice. In our laboratory, information geometry is applied to boosting to intuitively understand the behavior of the algorithms. Besides boosting algorithms, we apply information geometry to improve the accuracy of learning algorithms based on intuitive geometrical understandings.
(3) Optimization and Machine Learning
We study the applications of optimization techniques to machine learning algorithms.
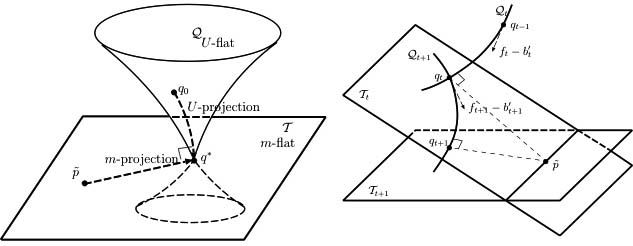
Figure : Information geometry of boosting
Career
- Takafumi Kanamori received a Ph. D. from the Graduate University for Advanced Studies, Japan in 1999.
- He joined the Department of Mathematical and Computing Sciences at Tokyo Institute of Technology as an Assistant Professor in 2001.
- In 2007 he moved to Nagoya University as an Associate Professor.
Academic Societies
- IEICE
- Japan Statistical Society
Publications
- Robust Estimation under Heavy Contamination using Unnormalized Models. Biometrika, 2015.
- Empirical Localization of Homogeneous Divergences on Discrete Sample Spaces. The Neural Information Processing Systems (NIPS), 2015.
- Density Ratio Estimation in Machine Learning, Cambridge University Press 2012.








