研究者総覧「情報知」
計算機数理科学専攻
- 氏 名
- 吉信 康夫(よしのぶ やすお)
- 講座等
- 情報数理基礎論講座
- 職 名
- 教授
- 学 位
- 博士(学術)
- 研究分野
- 数学基礎論 / 公理的集合論

研究内容
無限組合せ論と巨大基数公理
数学基礎論、特に公理的集合論を専門に研究している。なかでも、巨大基数公理と呼ばれる一連の公理群と、それに関連する無限組合せ論に興味をもっている。(1) 背景:巨大基数とは?
19世紀の終わり頃、ドイツの数学者カントルは、自然数全体の集合Nと実数全体の集合Rとの間には一対一対応が存在しないこと、その意味で無限の大きさ(濃度)には色々な種類があるということを発見した。以来、集合論という分野は、一言でいえば、色々な種類の無限濃度の組合せ的性質を明らかにすることを目標にして発展してきた。
最初の重要な問題として、カントルは、自然数全体の集合の濃度と実数全体の濃度の間に他の濃度は存在しないと予想した(連続体仮説:CH)が、証明できなかった。その後、このような問題を解決するために、またカントルの集合論は素朴過ぎてパラドックスを引き起こす恐れがあったこともあって、我々が無限集合について持っている直観的な認識を矛盾なく明確にするため、ツェルメロ、フレンケルらにより集合論の公理系ZFCが整備された。以後の集合論研究者はほとんどこの公理系に基づいて研究している。
ところが、ゲーデルとコーエンによって、CHはZFCからは真偽いずれとも決定できないことが証明されてしまったのである。これは、我々の無限集合についての認識が、この問題を解決するには不充分だという風にも考えられる。そこで、自然で説得力のある公理を追加して、この種の問題に決着をつけることが考えられる。ゲーデルは、強い性質を持った巨大な無限濃度の存在を仮定する(巨大基数公理)ことで、CHなどの独立命題が解決できるだろうと予想したのである。
結局、CHそのものについては、この予想は正しくなかったが、彼のアイデアは後の研究者達に受け継がれ、実数の集合のルベーグ可測性やベールの性質などに関するさまざまな命題が巨大基数公理から決定されることがわかってきた。このような事情により、巨大基数公理は今日の集合論の主要な研究対象の一つとなっている。
(2) 研究の概要
ここ数年私が特に興味をもって研究しているのは、巨大基数公理やその変種ともいえる強制公理がアレフ数2以上の基数における無限組合せ論の状況に与える影響、あるいは、関連することだが、これらの公理の、小さい基数には影響を与えないタイプの強制法(コーエンが連続体仮説の独立性証明において開発した、集合論のモデルをある種の拡大によって変形するきわめて一般的な手法)に対する保存性である。これらの諸公理が連続体の構造やω1に関する組合せ論に及ぼす影響はすでにかなりよく調べられており、より大きな基数における無限組合せ論への影響を考えることは自然な流れであるが、特にω2に関する組合せ論の場合、得られる結論の強さが仮定する強制公理の強さにかなり鋭敏に依存するなど、微妙で興味深い結果を得つつある。
例えば、最近ケーニヒとの共同研究で得た結果によれば、マーティンの極大公理MM(強制公理の一種)はω2閉な半順序集合による強制法で壊すことができるが、これより少し強いω2有向的閉な半順序集合による強制法では決して壊せないし、MMにかなり近い強制公理でもω2閉な半順序集合による強制法で保たれることがわかっている。
余談だが、これらの結果に、30年以上前に当時名大にいた難波完爾が導入したいわゆる難波強制法が本質的な役割を果たしていることには不思議な縁を感じる。
(3) 今後の展望
より長期的には、巨大基数公理の内部モデルの理論にも興味をもっている。巨大基数公理のもうひとつの特色として、それらは概ねその強さの順に線型に並んでおり、よく知られた無限組合せ論的命題の多くが、相対無矛盾の意味でこれらの公理のいずれかと同等になることが知られる、いわば命題の強さを測るものさしの役割を果たすという点にある。このような同等性の証明の片方は主に前述の強制法、つまりモデルの拡大による変形を用いて示される。そこでその逆を示すには、逆の操作、つまり縮小による巨大基数のモデルの構成を考えるのが自然である。内部モデルの理論とはそのような方法を与えるものである。しかし、強制法が集合論研究者の標準的手法として普及しているのに比べ、内部モデルの理論の研究は一握りの研究者たちのみの手で行われ、基礎的な文献が十分でなく、秘教のごとき様相を呈している。この事態を打開することが長期の目標である。
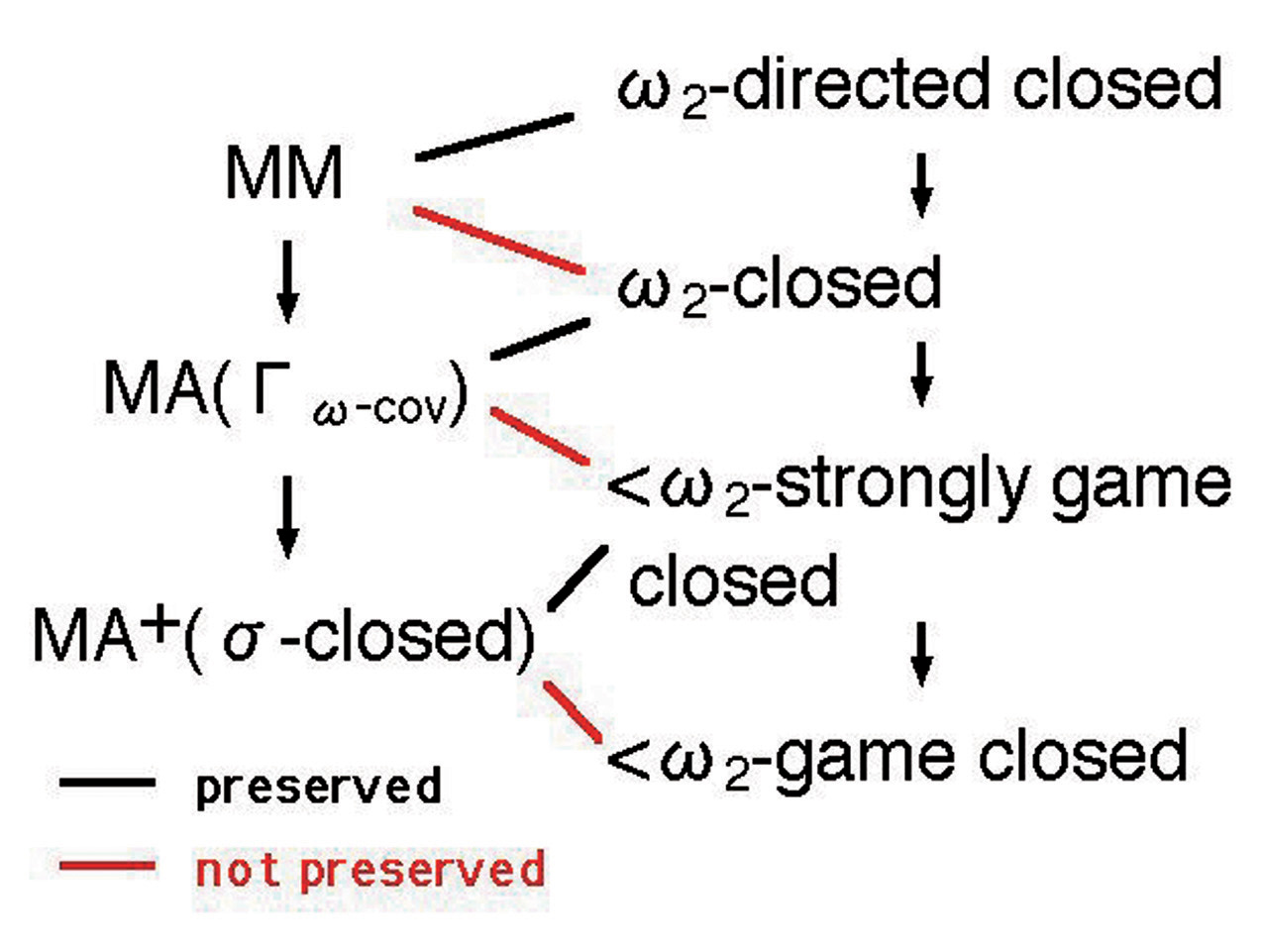
強制公理と半順序集合の階層構造の対応を表す図式
経歴
- 1995年名古屋大学大学院理学研究科博士課程(後期課程)中退、同大学院人間情報学研究科助手
- 2003年同大学院情報科学研究科助手
- 2005年より現職
- 2003年博士(学術)
- 1995年-1996年カリフォルニア大ロサンゼルス校訪問研究員
- 2002年-2003年文部科学省在外研究員(カリフォルニア大アーヴァイン校)
所属学会
- 日本数学会
主要論文・著書
- How many miles to βω ? - Approximating βω by metric-dependent compactifications (with M. Kada and K. Tomoyasu), Topology and its Applications 145, 2004.
- Fragments of Martin's Maximum in generic extensions (with B. König), Mathematical Logic Quarterly 50 (3), 2004.
- Approachability and games on posets, Journal of Symbolic Logic 68 (2), 2003.











